
こんにちは!
流体力学VTuberの流水うずまきです!
簡単なプロフィール

YouTubeで流体力学の解説をメインとして活動しています。
本日も流体力学を勉強していきましょう。

是非、「うずまきちゃん」って呼んでください。
“4つの流体力学” について

私は、学部生の講義を
“4つの流体力学”に分解し全体像を説明します
- 実測実験
- 管内流れ
- ポテンシャル流れ
- 粘性流体の流れ
“4つの流体力学” の特徴
“4つの流体力学”のゴール

4つの流体力学のゴールは、
「流れ場」「圧力場」「流体力」を、
「実測」または「机上計算」する事です
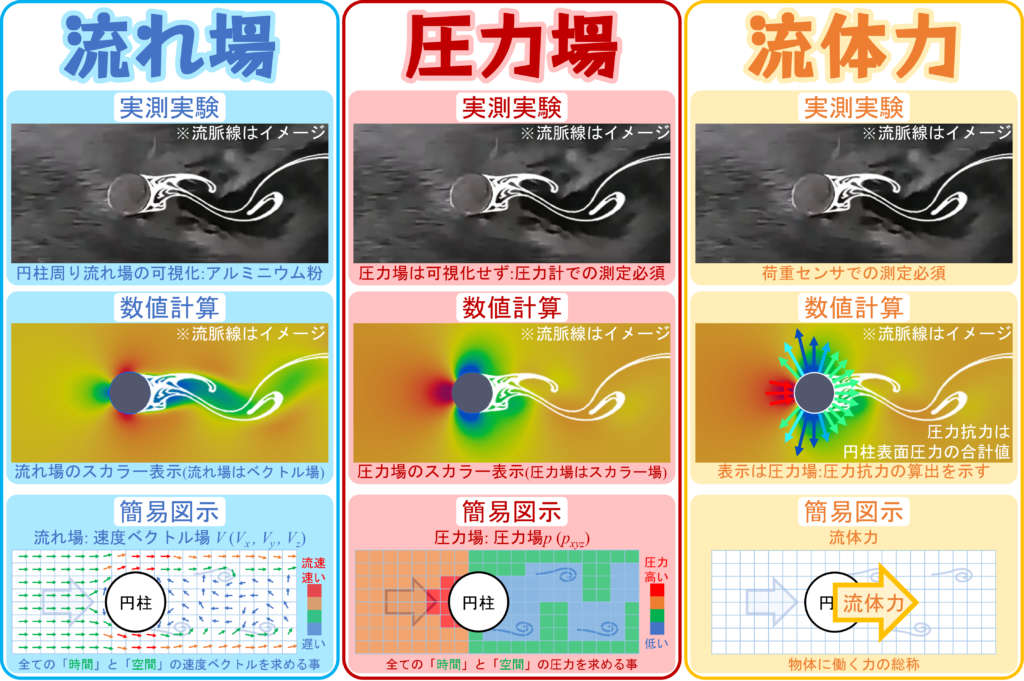
| 「流れ場/圧力場/流体力」と「実測実験/各机上計算」の対応付け(簡易表現) | |||
|---|---|---|---|
| 流れ場 | 圧力場 | 流体力 | |
| 場のカテゴリ | 速度ベクトル場 | 圧力スカラー場 | (場ではない) |
| 物理量 | u 流速[m/s] [ベクトル量] | p 圧力[Pa] [スカラー量] | F 力[N] (応力の場合もあり) |
| 1.実測実験 | 流速センサ (ピトー管,PIVなど) | 圧力センサ (圧力計など) | 荷重センサ (ロードセルなど) |
| 2.管内流れ | 連続の式 (場ではなく準1次元) | ベルヌーイの定理 (場ではなく1つ流線) | 運動量方程式 (場ではなく流体の塊) |
| 3.ポテンシャル流れ | 3D:ラプラス方程式 2D:複素ポテンシャル | 圧力方程式 | クッタ-ジューコフスキーの定理(揚力) |
| 4.粘性流体の流れ | 連続の式 (場の連続の式) | N-S方程式 | 流れ場と圧力場の 積分値(揚力,抗力) |

私の主張として、4つの流体力学は、
「それぞれ独立しており、各個撃破可能」と言うことです。
場とは?

場とは、
「空間分布」を見ることです。
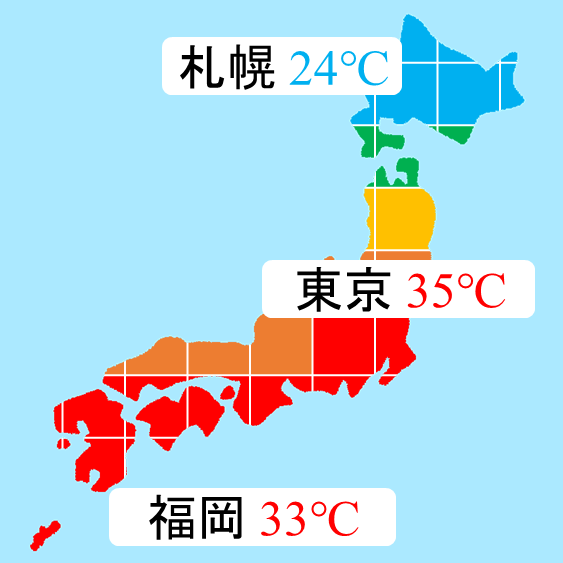
皆さんは台風が来た時、「遮蔽物」の有無で流速が変わることを経験していると思います。
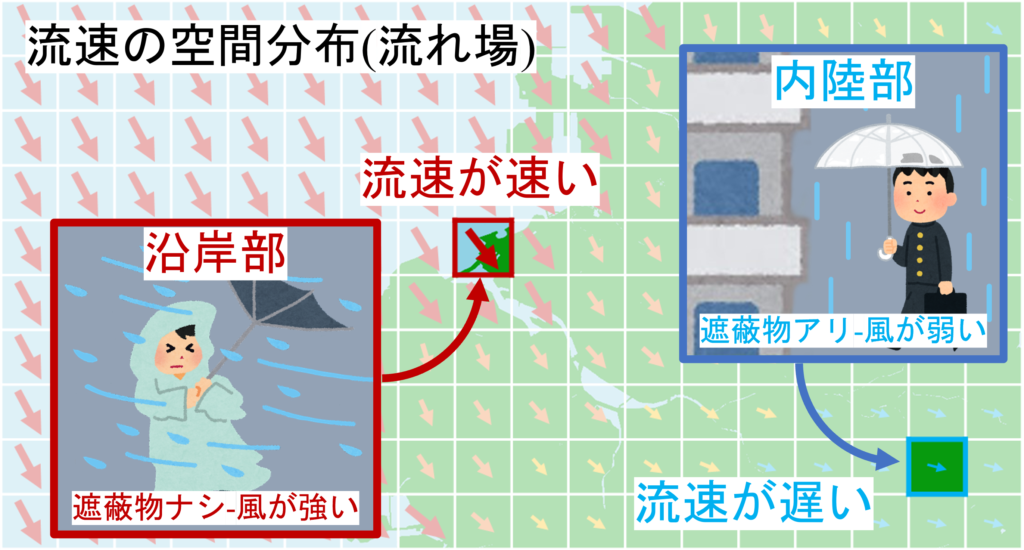
このように日常生活の中でも「流速が速い空間」と「流速が遅い空間」があり、
これを「流速の空間分布」=「流れ場」と言います。
いろいろな空間分布

代表的な場を示します。
全ての場が「空間分布」に着目しています。
| 流れ場 | 圧力場 | 温度場 | ||
| 流速の空間分布 | 圧力の空間分布 | 温度の空間分布 | ||
 |  |  | ||
| 地表面の2次元の流れ場 | 地表面の2次元の圧力場 | 地表面の2次元の温度場 | ||
| 流速の速い空間と遅い空間 | 圧力の高い空間と低い空間 | 温度の高い空間と低い空間 |
より正確に言えば、場とは「時間変化する空間分布」ですが、その説明は後に回します。
場の対義語(例:温度場)

「空間分布」の対義語は「一様分布」です。
| 「気温の空間分布」 | 「気温の一様分布」 | |
 |  | |
| 気温は空間分布があることが自然 | 気温の一様分布は、まずありえない |
下記のサーモグラフィ画像に示すように、日常生活中では、温度には空間分布がある事が「当たり前」と言え、むしろ温度が一様なものを探す方が難しいです。
| 温度場 |
| サーモグラフィによる温度の空間分布の実測結果 |
 |
「ベクトル場」と「スカラー場」の違い

「矢印で表されるのがベクトル量」です。
| ベクトル量 | スカラー量 | |||
| 「向き」と「大きさ」を持った量 | 「大きさ」のみ持った量 | |||
| 物理量 : 流速, 加速度, 力, 運動量 | 物理量 : 圧力, 温度, エネルギー | |||
| 流速 [m/s] (ベクトル量) | 圧力 [Pa] (スカラー量) | |||
| 向き | 風向き [角度°] | 向き | × | |
| 大きさ | 流速 [m/s] | 大きさ | 圧力 [Pa] | |
| 流れ場 (速度ベクトル場) | 圧力場 (圧力スカラー場) | |||
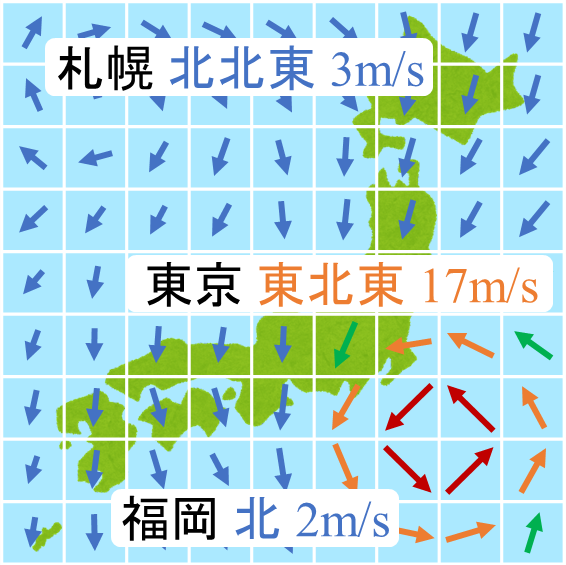
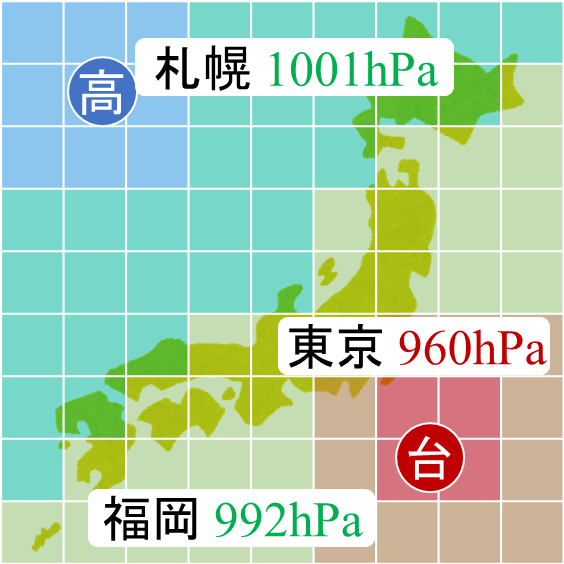
 |  | |||
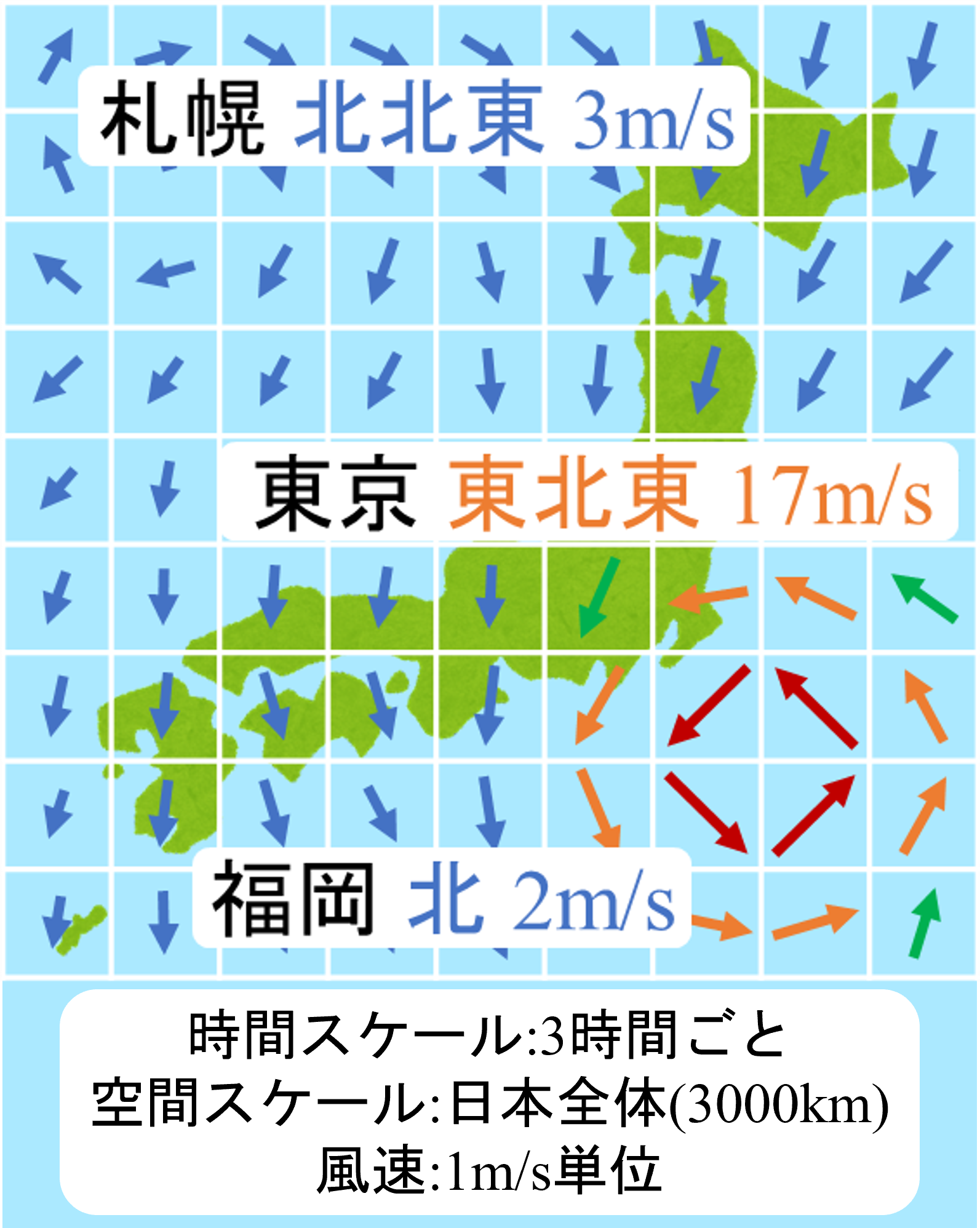
| 地表面の2次元の流れ場 (風速[m/s]) | 地表面の2次元の圧力場 (大気圧[hPa]) | |||
| 例:東北東の風 17 [m/s] (風向きと流速を指定している-ベクトル場) | 例:台風の中心気圧は960 [hPa] (圧力のみ指定し向きを指定せず-スカラー場) | |||
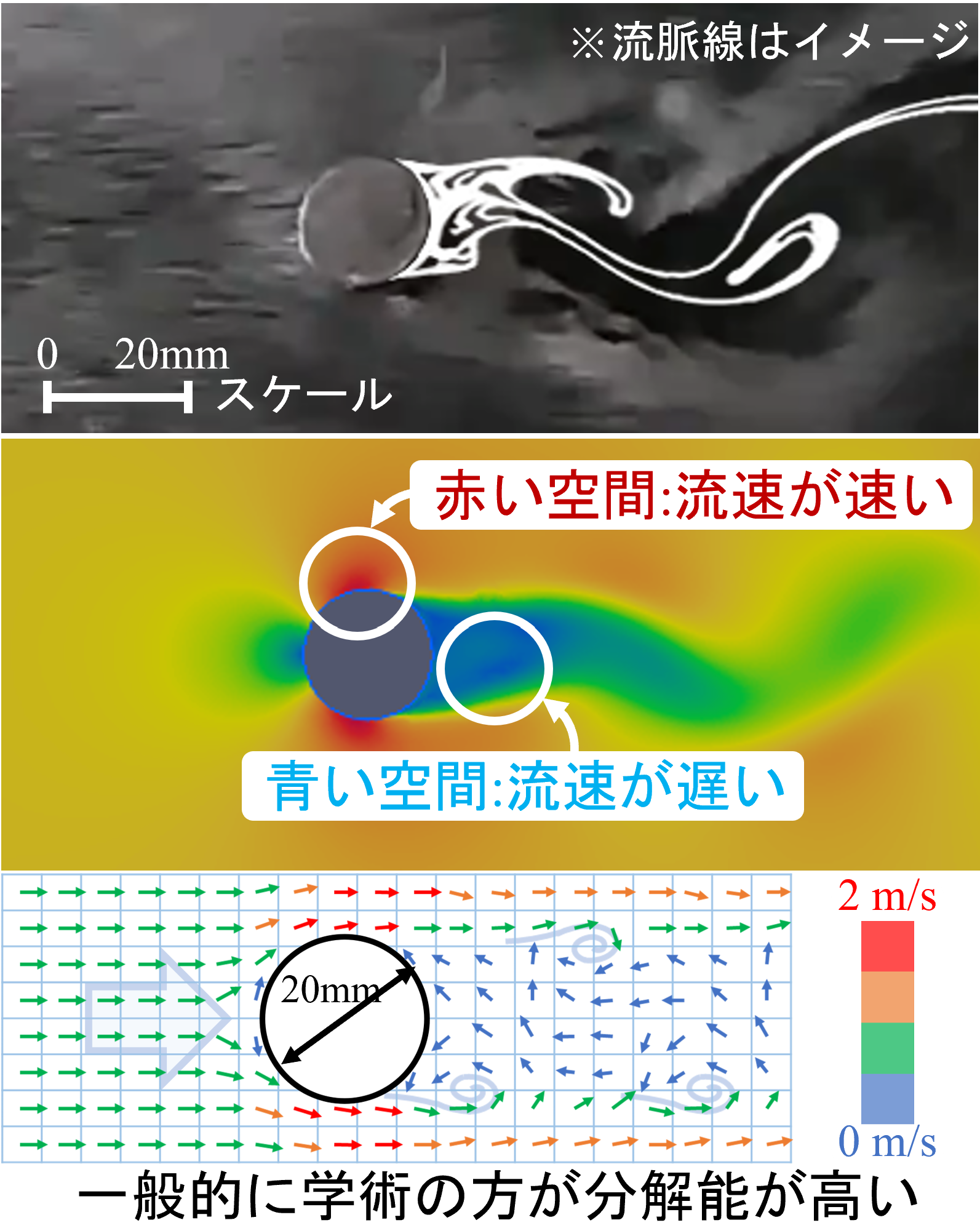
流体力学における場の分解能

流体力学の場は
特に「時間/空間/物理量の分解能」を上げて現象を観察します。
「日常生活の感覚」と「流体力学の解像度」の違いとして、「分解能」が挙げられます。
学問的になるほど、分解能を上げた「より詳細な物理現象の観察」が重要となり、「時間分解能」「空間分解能」「物理量分解能」を細かくする傾向があります。
「日常生活の感覚」と「流体力学の解像度」の違い(概要)
| 各分解能 | 日常生活の感覚 | 流体力学の解像度 | ||
| “時間”分解能 | 3時間ごと | → | 0.1秒ごと | |
| “空間”分解能 | 100km間隔 | → | 1cm間隔 | |
| “物理量”分解能 | 流速 1m/s刻み | → | 流速 0.1m/s刻み |
| 日常生活の感覚 | 流体力学の解像度 | |||
| スケールの大きいな空間分布 | スケールの小さい(局所的)な空間分布 | |||
| 例:全国の天気 | 例:円柱周りの流れ場 | |||
| 時間感覚 | 3時間ごと | 時間分解能 | 0.1秒 | |
| 空間感覚 | 100km程度 | 空間分解能 | 1cm | |
| 物理量感覚 | 風速1 m/s 単位 | 物理量分解能 | 0.1m/s 単位 | |
 |  | |||
教室の温度は1つか?

先生!
エアコンが寒いので切ってもいいですか?
教室内で賛否両論が起こる、夏によくある会話ですが、
この揉め事には「1つの設定温度」と「温度の空間分布(温度場)」が密接に関わります。
| リモコン | 教室内の実態 | ||
| 設定温度 (1つの温度) | 温度の空間分布 (無数の温度) | ||
 | 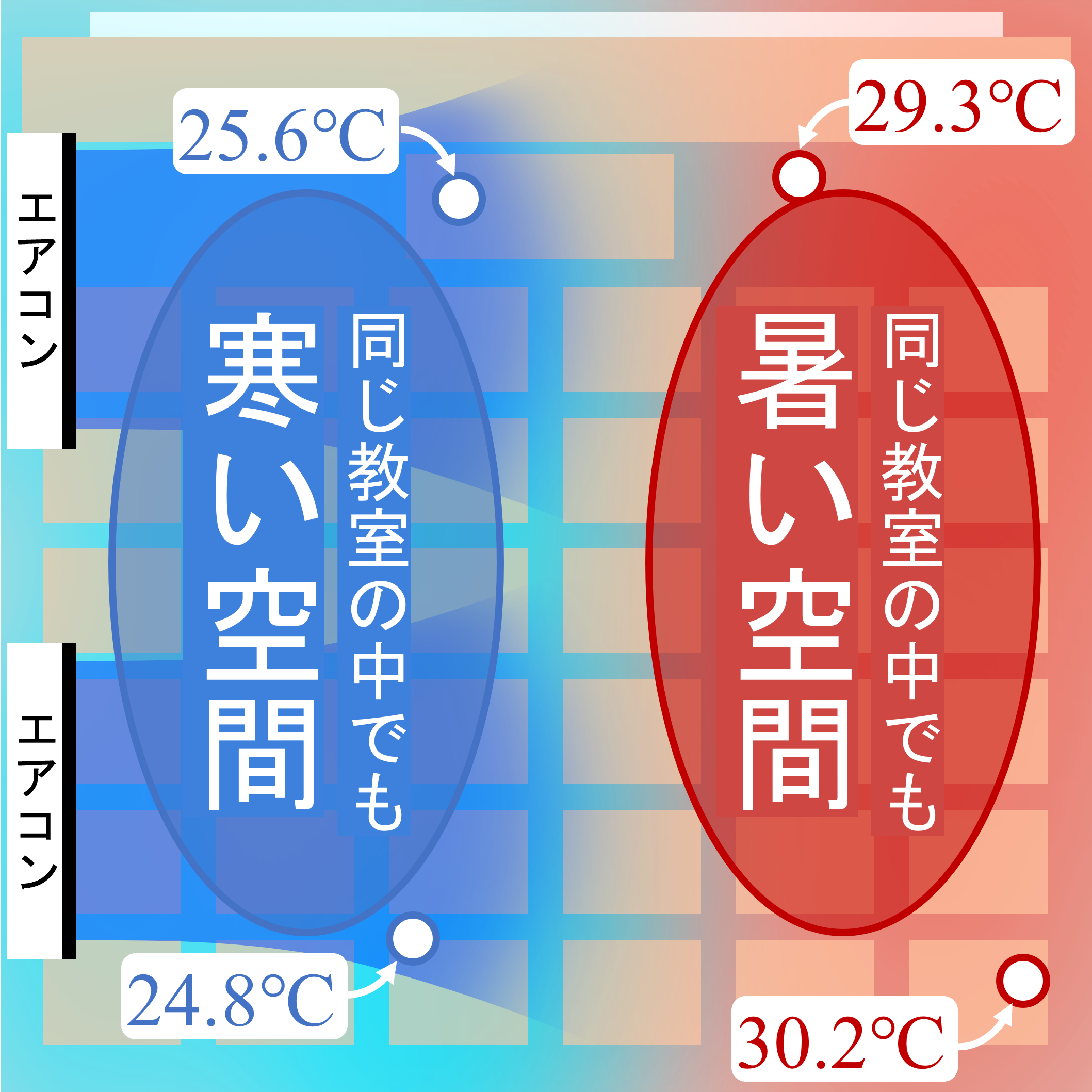 | ||
リモコンは1つの温度ですが、同じ教室内でも、空間によって温度が異なります。
このような「教室の中など、比較的小さいスケールにおける局所的な温度の空間分布(温度の空間的な偏り)」を見るのが対流熱伝達です。
札幌と那覇では「気候が異なる」と言う明確な温度の空間分布の依拠がありますが、教室内のような比較的小さなスケールでも温度場は存在し、実際にエアコンを止める/止めないの争いに発展するほど、「細かな温度の空間分布」を観察することは重要です。
流れ場とは?
流れ場の基礎

流れ場とは
「時間/空間/物理量の分解能」を上げた「流速の空間分布」の観察です。
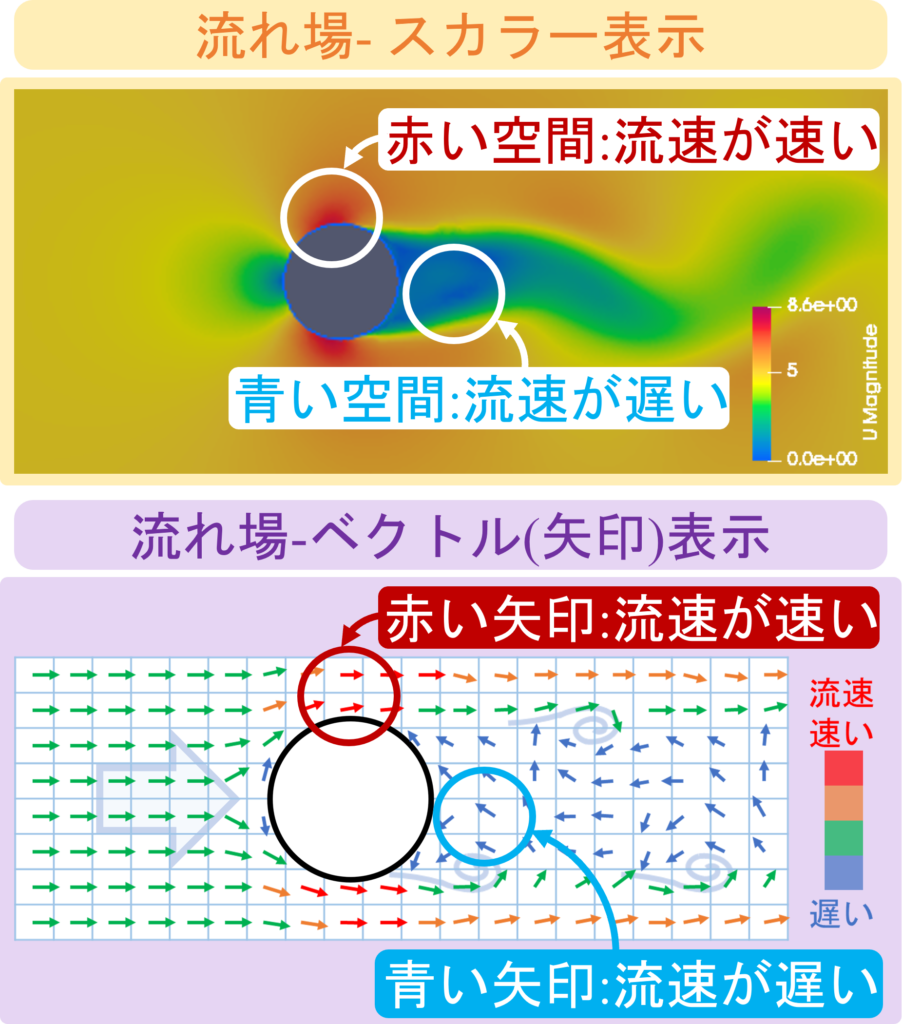
流れ場は「連続した空間」について「流速の速い空間」と「流れの遅い空間」に着目します。
流れ場の空間領域の分類-基礎

主に流れ場は、
「2つの空間領域に分類」する事が可能です。
この空間の領域分けは、境界層理論の最も簡単な図示表現です。
| 「粘性を考慮しない空間」と「粘性を考慮すべき空間」 |
  |

境界層理論は、
「ポテンシャル流れ」と「粘性流体の流れ」を
「領域分けによって繋げた理論(漸近理論)」と言えます。
粘性を考慮しない空間領域→理想流体→理想流体の理論→「ポテンシャル流れ」
粘性を考慮すべき空間領域→粘性流体→粘性流体の理論→「粘性流体の流れ」

流れ場の空間領域の分類-応用

さらに流れ場は、
「5つの空間領域に分類」する事が可能です。
この空間の領域分けは、境界層理論の最も簡単な図示表現です。


| 流れ場の5つの空間領域の分類 | ||||
| 1.粘着境界条件 |  | |||
| 固体物体と流体の接触境界の空間(に関する条件) | ||||
| 粘性流体の場合 | 粘着境界条件 | 固体接触面で流速ゼロ | ||
| 理想流体の場合 | 非粘着境界条件 | 固体接触面で流速が存在 | ||
| 2.境界層 |  | |||
| 粘性の影響により、流速が「主流速の99%以下」の空間 | ||||
| 粘性流体の場合 | Re数が大きい流れは境界層が薄く境界層方程式が成立 | |||
| 理想流体の場合 | 理想流体の流れに境界層は存在しない | |||
| 3.境界層剥離点 |  | |||
| 粘性の影響により、物体背面からの逆流により境界層が剥離する点 | ||||
| 粘性流体の場合 | ほとんどの物体で境界層剥離は起こる(特に鈍頭物体) | |||
| 理想流体の場合 | 理想流体の流れに境界層剥離点は存在しない | |||
| 4.伴流領域 |  | |||
| 粘性の影響により、物体背面の逆流から複雑な渦が生じている空間 | ||||
| 粘性流体の場合 | ほとんどの物体で伴流領域を形成する(特に鈍頭物体) | |||
| 理想流体の場合 | 理想流体の流れに伴流領域は存在しない | |||
| 5.理想流体領域 |  | |||
| 粘性の影響を受けづらく、理想流体とみなせる空間 | ||||
| 粘性流体の場合 | 境界層、伴流領域の外は粘性を考慮しなくて良い | |||
| 理想流体の場合 | 固体物体以外の流体空間全てが粘性を考慮しない | |||
圧力場とは?

圧力場とは、
「時間/空間/物理量の分解能」を上げた「圧力の空間分布」の観察です。
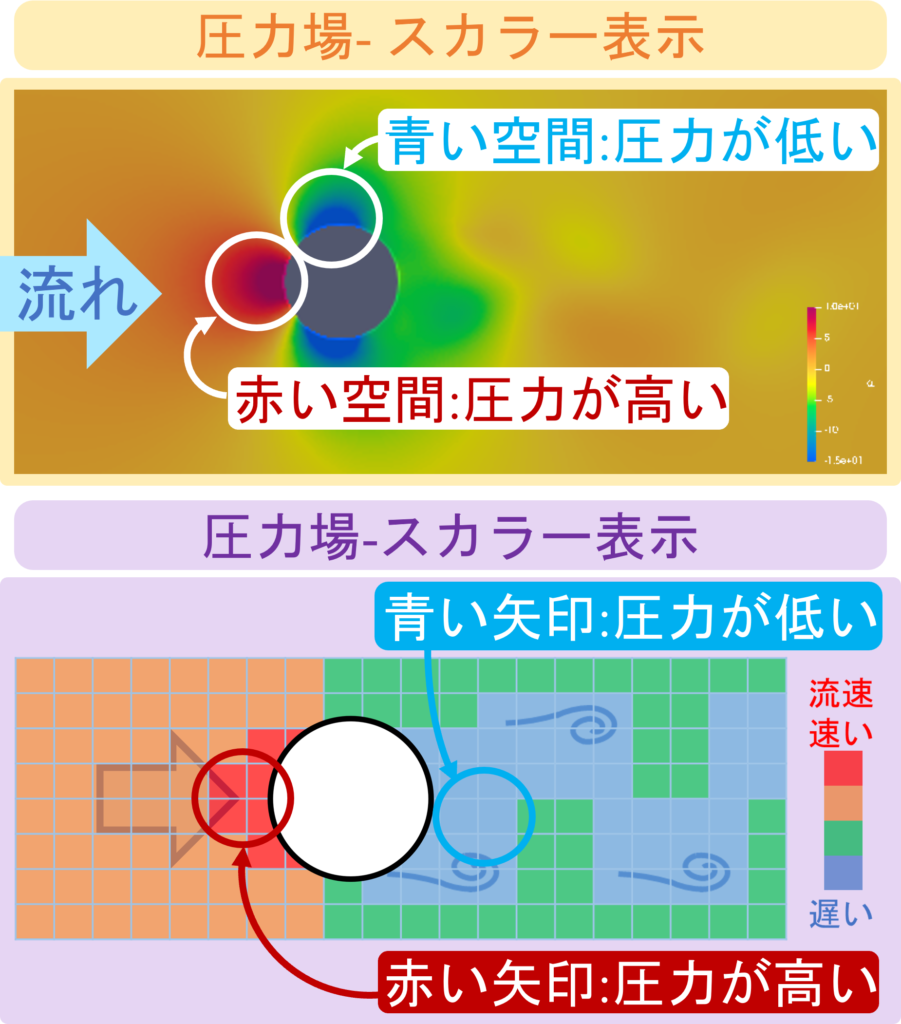
圧力場は「連続した空間」について
「圧力の高い空間」と「圧力の低い空間」の「分布」に着目します。
その他の場
その他の場としては、「変形場」「応力場」「温度場」「磁場」「電場」などがあります。
場とは?の投稿記事のリンクを貼る。
私としては、「全流体力学のゴール」は「流れ場」「圧力場」「流体力」 とまで主語を大きくしたいですが、下記のような例外があり、一旦 “4つの流体力学” に留めておきます。
流体力学:「流れ場」「圧力場」「流体力」
熱流体:「流れ場」「圧力場」「流体力」+「温度場」
レオロジー:「流れ場」「圧力場」「流体力」+「応力場(第一法線応力差など)」
流体力

流体力とは、
「流体の運動によって物体に働く力の総称」をであり
「揚力」と「抗力」が挙げられます。
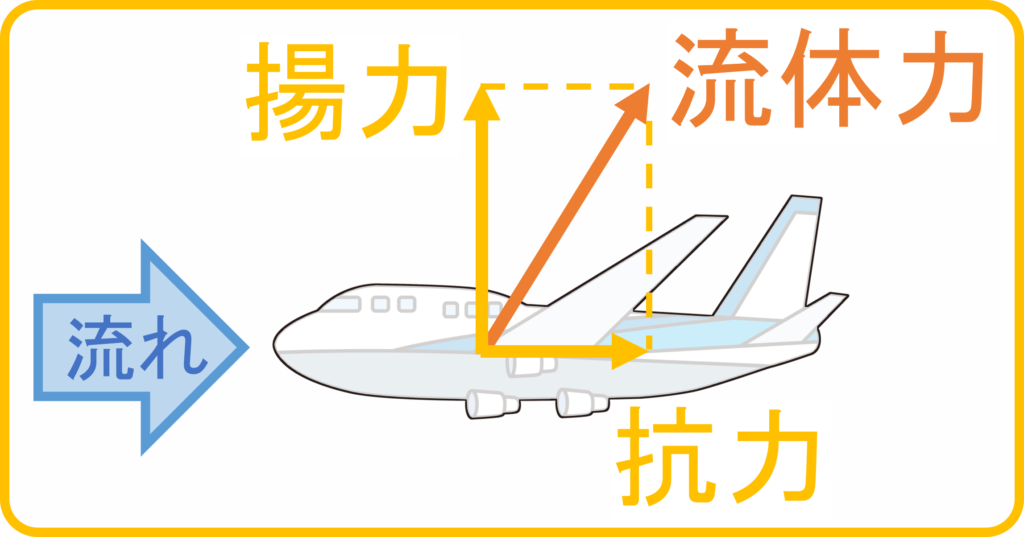
流体力は、流体の運動によって物体に働く力の総称です。
実測/机上計算
“4つの流体力学”の結論

4つの流体力学の結論は、
「理想流体」と「粘性流体」の違いを見ることです
“4つの流体力学” の依拠
“4つの流体力学” の概要
1.実測実験
2.管内流れ
3.ポテンシャル流れ
4.粘性流体の流れ
まだまだある-少なくとも7つの主要流体力学

学部生の基礎に限らなければ、
少なくともさらに”7つの流体力学”が挙げられます
- 水の波
- 濡れ性
- レオロジー
- 圧縮性流体力学
- 宇宙流体力学
- 一般相対論的電磁流体力学/一般相対論的輻射流体力学
- 量子流体力学
現在、記事の作成中です。
しばらくお待ちください。(2024年2月頃完成予定)
固定ページ 流水うずまき


もちろん、4つの流体力学は、全て同じ流体力学であるため、基本的な考え方は同様です。特に「流れ場」「圧力場」「流体力」を求めると言う点では一致しています。
ここまで流体力学は繋がっていると言う前置きをした後で、私の主張をします。
「4つの流体力学は、順不同であり、どれから学んでも良いです」
各場と各方程式に示すように、重なっている方程式はありません。
大学講義のテストで点数を取るだけなら、4つの流体力学は全くの別物と考えた方が自然です。