
流水うずまき
「流れ場」とは「圧力場」「流体力」と合わせ、
”流体力学のゴールの1つ”と言えます。
前回までの場の説明

流水うずまき
前回、場の基礎について説明しました。
よければこちらの記事から参照してください。

流水うずまき
私のblog全体の目次です。
よければこちらの記事から参照してください。
流れ場の基礎

流水うずまき
流れ場とは
「時間/空間/物理量の分解能」を上げた「流速の空間分布」の観察です。
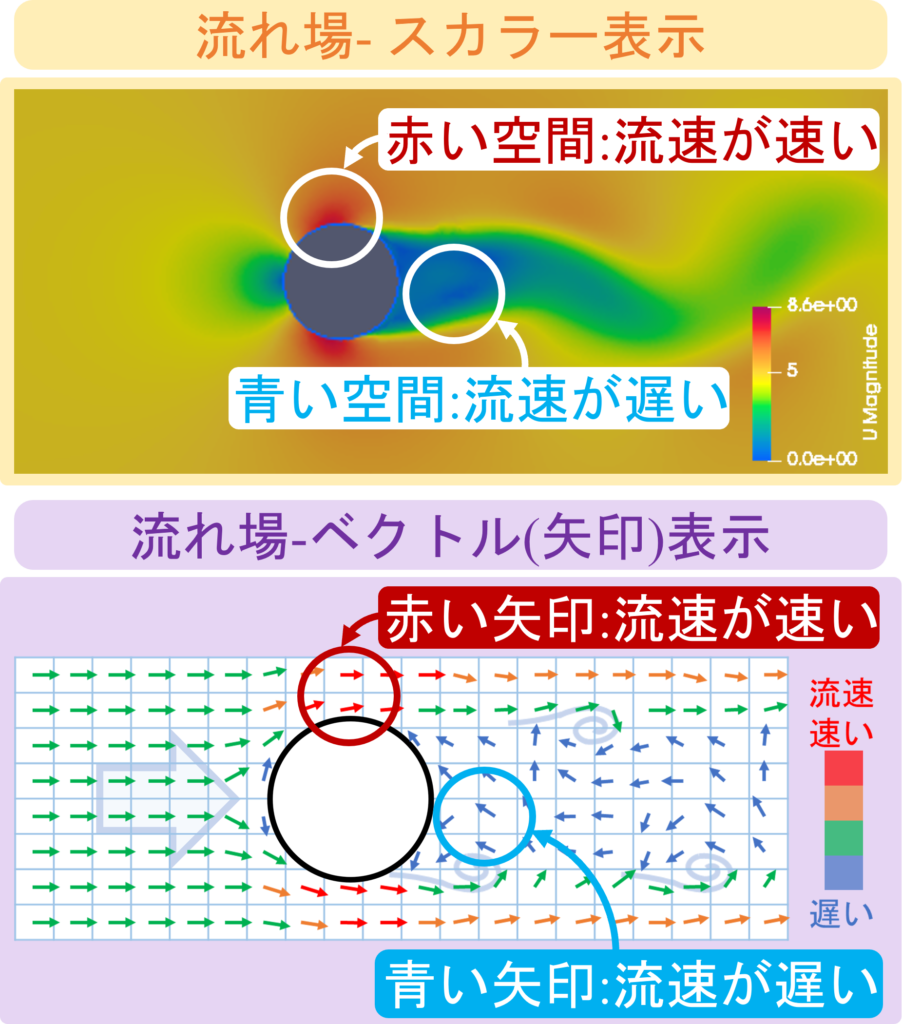
流れ場は「連続した空間」について
「流速の速い空間」と「流れの遅い空間」の「分布」に着目します。
2つの流れ場領域

流水うずまき
主に流れ場は、
「2つの空間領域に分類」する事が可能です。
この空間の領域分けは、境界層理論の最も簡単な図示表現です。
| 「粘性を考慮しない空間」と「粘性を考慮すべき空間」 |
  |

流水うずまき
境界層理論は、
「ポテンシャル流れ」と「粘性流体の流れ」を
「領域分けによって繋げた理論(漸近理論)」と言えます。
ポテンシャル流れの空間領域
粘性を考慮しない空間領域→理想流体→理想流体の理論→「ポテンシャル流れ」
粘性流体の流れの空間領域
粘性を考慮すべき空間領域→粘性流体→粘性流体の理論→「粘性流体の流れ」

5つの流れ場領域

流水うずまき
さらに流れ場は、
「5つの空間領域に分類」する事が可能です。
この空間の領域分けは、境界層理論の最も簡単な図示表現です。


| 流れ場の5つの空間領域の分類 | ||||
| 1.粘着境界条件 |  | |||
| 固体物体と流体の接触境界の空間(に関する条件) | ||||
| 粘性流体の場合 | 粘着境界条件 | 固体接触面で流速ゼロ | ||
| 理想流体の場合 | 非粘着境界条件 | 固体接触面で流速が存在 | ||
| 2.境界層 |  | |||
| 粘性の影響により、流速が「主流速の99%以下」の空間 | ||||
| 粘性流体の場合 | Re数が大きい流れは境界層が薄く境界層方程式が成立 | |||
| 理想流体の場合 | 理想流体の流れに境界層は存在しない | |||
| 3.境界層剥離点 |  | |||
| 粘性の影響により、物体背面からの逆流により境界層が剥離する点 | ||||
| 粘性流体の場合 | ほとんどの物体で境界層剥離は起こる(特に鈍頭物体) | |||
| 理想流体の場合 | 理想流体の流れに境界層剥離点は存在しない | |||
| 4.伴流領域 |  | |||
| 粘性の影響により、物体背面の逆流から複雑な渦が生じている空間 | ||||
| 粘性流体の場合 | ほとんどの物体で伴流領域を形成する(特に鈍頭物体) | |||
| 理想流体の場合 | 理想流体の流れに伴流領域は存在しない | |||
| 5.理想流体領域 |  | |||
| 粘性の影響を受けづらく、理想流体とみなせる空間 | ||||
| 粘性流体の場合 | 境界層、伴流領域の外は粘性を考慮しなくて良い | |||
| 理想流体の場合 | 固体物体以外の流体空間全てが粘性を考慮しない | |||
流れ場と方程式の関係
| 「流れ場/圧力場/流体力」と「実測実験/各机上計算」の対応付け(簡易表現) | |||
|---|---|---|---|
| 流れ場 | 圧力場 | 流体力 | |
| 場のカテゴリ | 速度ベクトル場 | 圧力スカラー場 | (場ではない) |
| 物理量 | u 流速[m/s] [ベクトル量] | p 圧力[Pa] [スカラー量] | F 力[N] (応力の場合もあり) |
| 1.実測実験 | 流速センサ (ピトー管,PIVなど) | 圧力センサ (圧力計など) | 荷重センサ (ロードセルなど) |
| 2.管内流れ | 連続の式 (場ではなく準1次元) | ベルヌーイの定理 (場ではなく1つ流線) | 運動量方程式 (場ではなく流体の塊) |
| 3.ポテンシャル流れ | 3D:ラプラス方程式 2D:複素ポテンシャル | 圧力方程式 | クッタ-ジューコフスキーの定理(揚力) |
| 4.粘性流体の流れ | 連続の式 (場の連続の式) | N-S方程式 | 流れ場と圧力場の 積分値(揚力,抗力) |





コメント